数独の問題作成をpythonで作りたい vol.5

勉強しているとこの近くにいいお店があって、

お昼はよくチキンオーバーライスを食べています。超絶美味しいです。しかも、ワンコイン！500円です！

https://stayhungry.shopinfo.jp/

今日は一番難しいかなーと思っていた数独の解くプログラムです。

前回の続きとなります。前回は空きマスを作ったところまででしたね。

それでは早速見ていきましょう！

今日やったこと

• 数独を解く関数の実装

方針

どうやって解いていけばいいか悩んだところ、以下の方法でやっていくことにしました。

• 0が入っている位置を列挙リストする
• 列挙リストの中から一個ずつ取り出す。
• 横列と縦列とブロックでルール上挿入することができない数字リストを作成する。
• 上記を裏返して、挿入できる数字リストを作成する。
• 挿入できる数字リストの中身が1個だけだったら確定なので、挿入する。
• 1個以上ならば列挙リストの最後尾に再登録する。
• 列挙リストにデータが無くなったら終わり。
• 無限ループになっていると判断したら終わり。

ソースコード

例のごとく長いので、適宜読み飛ばしてくださいね。下で詳細を書いています。

import numpy as np
from sudoku import Sudoku as Sudoku

"""
 
             _                  _               
            | |                | |              
   ___  ___ | |_   _____    ___| | __ _ ___ ___ 
  / __|/ _ \| \ \ / / _ \  / __| |/ _` / __/ __|
  \__ \ (_) | |\ V /  __/ | (__| | (_| \__ \__ \
  |___/\___/|_| \_/ \___|  \___|_|\__,_|___/___/
                                                
                                                
 
"""
class Solve(Sudoku):
    def __init__(self,_table):
        self.question = np.array(_table)
        self.answer = np.copy(self.question)
        self.result = False
        self.solve(self.question)
        
    def solve(self,_table):
        table = np.copy(_table)
        zero_position = self.get_zero_position(_table)
        print(zero_position)
        loop_count = 0
        while len(zero_position) > 0 and len(zero_position) >= loop_count - 5:
            target_position = zero_position.pop(0)
            uninsertable = np.concatenate(
                                            (
                                                self.get_uninsertable_by_row(table,target_position),
                                                self.get_uninsertable_by_column(table,target_position),
                                                self.get_uninsertable_by_block(table,target_position),
                                            ),
                                            axis=None
                                        )
            uninsertable = np.unique(uninsertable)
            insertable = []
            for i in range(1,10,1):
                if not i in uninsertable:
                    insertable.append(i)
            if len(insertable) == 1:
                table[target_position[0]][target_position[1]] = insertable[0]
                loop_count = 0
            else:
                zero_position.append(target_position)
                loop_count += 1
        print(self.get_zero_position(table))
        if not self.get_zero_position(table):
            self.result = True
        else:
            self.result = False    
        self.answer = np.copy(table)
    
    def get_zero_position(self,_table):
        result = []
        for i in range(9):
            for j in range(9):
                if not _table[i][j]:
                    result.append([i,j])
        return result
    
    def get_uninsertable_by_row(self,_table,pos):
        result = []
        for i in range(1,10):
            if i in _table[pos[0]]:
                result.append(i)
        return result

    def get_uninsertable_by_column(self,_table,pos):
        _table = _table.T
        result = []
        for i in range(1,10):
            if i in _table[pos[1]]:
                result.append(i)
        return result

    def get_uninsertable_by_block(self,_table,pos):
        _table = _table[(3*(pos[0]//3)):(3*(pos[0]//3)+3) , (3*(pos[1]//3)):(3+3*(pos[1]//3))]
        _table = np.reshape(_table,9)
        result = []
        for i in range(1,10):
            if i in _table:
                result.append(i)
        return result

    def display_result(self,_table):
        if self.result and self.test_format(_table):
            print("### solve ###")
        else:
            print("xxx not solve xxx")

手始めにSolveクラスとsolve関数を用意しました。

class Solve(Sudoku):
    def __init__(self,_table):
        self.question = np.array(_table)
        self.answer = np.copy(self.question)
        self.result = False
        self.solve(self.question)
        
    def solve(self,_table):

solve関数で問題を解いていく感じにしようかなと思います。

ソースコードと前後しますが、solve関数で必要なものを用意します。

まず一つ目、0が入っている場所を返す関数

if not で0=偽の時を真にして、resultに追加しています。

def get_zero_position(self,_table):
        result = []
        for i in range(9):
            for j in range(9):
                if not _table[i][j]:
                    result.append([i,j])
        return result

二つ目、横の行にある数字を返す関数

def get_uninsertable_by_row(self,_table,pos):
        result = []
        for i in range(1,10):
            if i in _table[pos[0]]:
                result.append(i)
        return result

こっちは1〜9まで準備横列にあったら追加しています。

今思うと0を除くメソッドとか使っても良かったかもしれません。Rubyにはありますよねそんなメソッド

def get_uninsertable_by_column(self,_table,pos):
        _table = _table.T
        result = []
        for i in range(1,10):
            if i in _table[pos[1]]:
                result.append(i)
        return result

    def get_uninsertable_by_block(self,_table,pos):
        _table = _table[(3*(pos[0]//3)):(3*(pos[0]//3)+3) , (3*(pos[1]//3)):(3+3*(pos[1]//3))]
        _table = np.reshape(_table,9)
        result = []
        for i in range(1,10):
            if i in _table:
                result.append(i)
        return result

縦列とブロックもほぼほぼ同じ流れです。

ブロックはnumpyのスライスを使って、うまいこと9マスのブロックを取り出すことができました。

posにはsolve関数から呼ばれるその時点で調べているマスの座標が入ってきます。

def solve(self,_table):
        table = np.copy(_table)
        zero_position = self.get_zero_position(_table)
        print(zero_position)
        loop_count = 0
        while len(zero_position) > 0 and len(zero_position) >= loop_count:
            target_position = zero_position.pop(0)
            uninsertable = np.concatenate(
                                            (
                                                self.get_uninsertable_by_row(table,target_position),
                                                self.get_uninsertable_by_column(table,target_position),
                                                self.get_uninsertable_by_block(table,target_position),
                                            ),
                                            axis=None
                                        )
            uninsertable = np.unique(uninsertable)
            insertable = []
            for i in range(1,10,1):
                if not i in uninsertable:
                    insertable.append(i)
            if len(insertable) == 1:
                table[target_position[0]][target_position[1]] = insertable[0]
                loop_count = 0
            else:
                zero_position.append(target_position)
                loop_count += 1
        print(self.get_zero_position(table))
        if not self.get_zero_position(table):
            self.result = True
        else:
            self.result = False    
        self.answer = np.copy(table)

solveは長いですが、変数を理解すれば読み解けるはずです。

table ・・・　解く問題の二次元配列
zero_position ・・・ 0が入っている未入力の場所一覧が入った配列
loop_count ・・・ ループカウンタ　zero_positionの大きさよりもループしてたら無限ループとみなし、解くことができないとし、終了します。
target_position ・・・　今から解く未入力の場所
uninsertable ・・・　ルール上、挿入できない数字のリスト
insertable ・・・　挿入できる数字のリスト

uninsertableのリストからinsertableを生成しています。もし、insertableの長さが1つだけだった場合は、その数字で確定するので、挿入！

そうでなければzero_positionの最後尾に入れ直すことにしました。

zero_positionは若い方から順にpopされていくので、うまくいけば空配列になり、問題が解けた状態になります。

今日の成果物

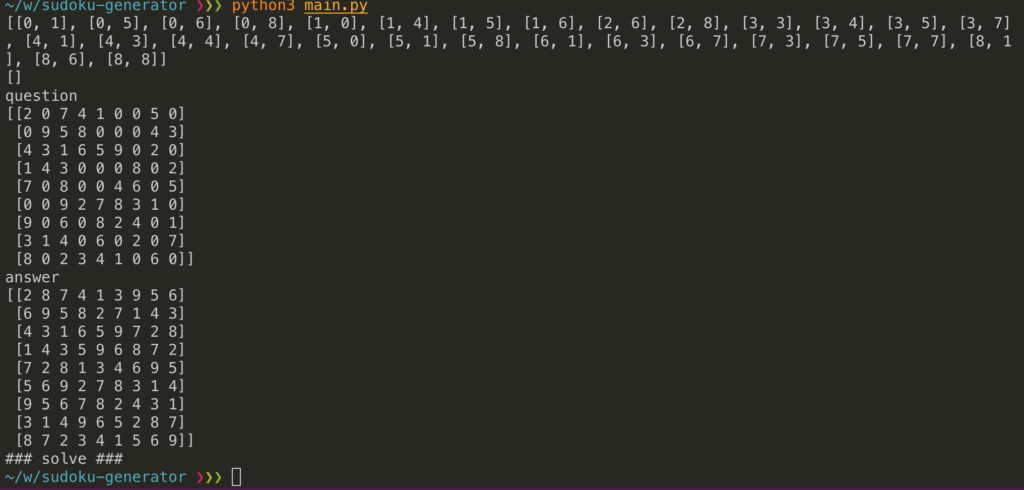
画像の一番上がzero_positionの一覧です。[0,1]は上から0番目左から1番目を表しています。

次の配列[]は、終了時の中身です。問題が解けなかった場合はここにzero_positionが残ります。

結果の見方は言わずもがなですね。

まだ足りないこと

下絵の(0,0)要素をみてください。人間なら即 “7” ってわかりますね。

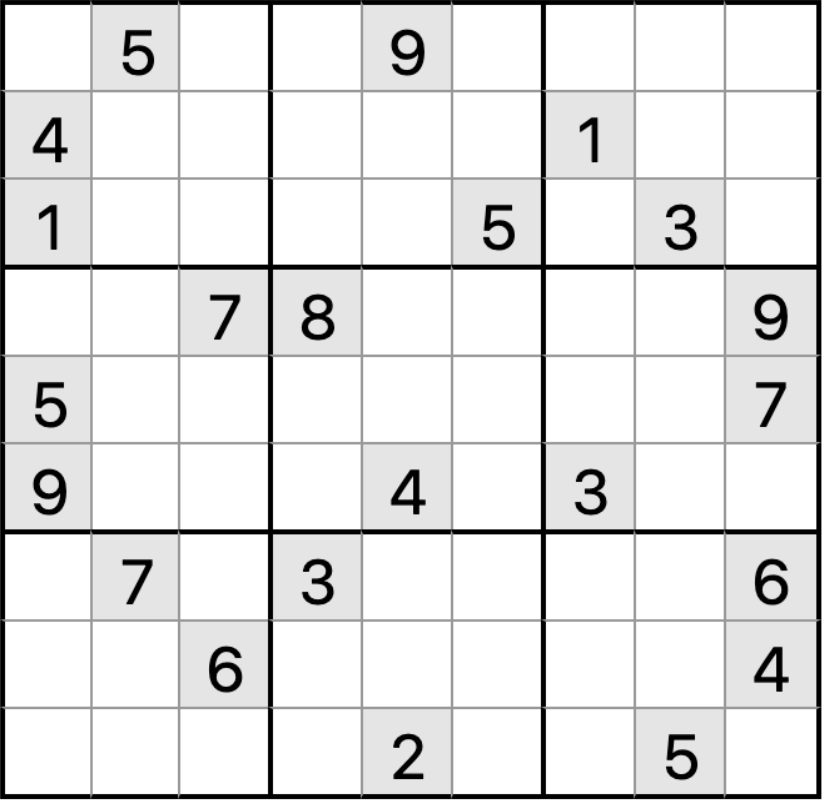
でも、私のプログラムだと、(0,0)はinsertable[2,3,6,7,8]となるわけですので、zero_positionの最後尾に後でやるアイテムとして登録されてしまうのです。

どうにか上手いことできないかと考えましたが、今日時点では難しかったです。

いいアイデア求む！

結果どんな問題を生成できるか

先日から踏まえて、解答を作成できるようになりました。そして0を入れることができました。そして問題を解いて妥当性を確認できるようになりました。

解答は全数独のうち全数独を生成できます。

0は20〜30個までなら解いて妥当性を確認できますが、40、50個となるとソルバー関数が弱いので検証できないです。

0もランダムで入れているため、右とか左に偏ったりしてしまい、解が一意に決まらなくなってしまうことがしばしばです。

まとめ

前項で述べたとおり、ソルバー関数が弱いので、いずれDeepLearningで精度よく解けるかやってみたいです。

とりあえず完成させたいので、このまま進めていきます。

難しい部分でしたが、全部自分で考えて実装できたので、すごい成長した気がします。

今までのSudokuクラス、Solveクラスをみたい方は、以下Githubまで！！

フォローもしてくれると嬉しいです。

https://github.com/ratovia/sudoku-generator