ABC129のB問題を解いたので、思考プロセスを載せておきます
Contents
問題文
11 から NN の番号がついた NN 個の重りがあり、番号 ii の重りの重さは WiWi です。ある整数 1≤T<N1≤T<N に対してこれらの重りを、番号が TT 以下の重り と 番号が TT より大きい重りの 22 グループに分けることを考え、それぞれのグループの重さの和を S1,S2S1,S2 とします。このような分け方全てを考えた時、S1S1 と S2S2 の差の絶対値の最小値を求めてください。
https://atcoder.jp/contests/abc129/tasks/abc129_b
ACしたコード
### SNIPPET
# n = gets.split.map(&:to_i)
# array = n.times.map { gets.split.map(&:to_i) }
# [].all?(&:even?)
# a = [*1..m].repeated_combination(n).to_a
# [1,2,3,4,5].select { |num| num.even? } # => [2, 4]
# ["a","a","b"].group_by(&:itself).map{|k,v| [k, v.count]}.to_h #=> {"a"=>2, "b"=>1}
# 切り捨て: .floor(2).to_f ,切り上げ: .ceil(2).to_f,四捨五入: round(2)
# 3.upto(6) do |i|, 6.downto(3) do |i|
# 公約数125.gcd(100)、公倍数125.lcm(100)
# PI = Math::PI
# 高さ = a * Math.sin(w / 180.0 * Math::PI), 底辺 = a * Math.cos(w / 180.0 * Math::PI)
# def chmax(a, b) a > b ? a : b end
INF = Float::INFINITY
def chmin(a, b) a < b ? a : b end
n = gets.to_i
w = gets.split.map(&:to_i)
s = Array.new(w.size+1,0)
n.times do |i|
s[i+1] = s[i] + w[i]
end
min = INF
1.upto(n) do |i|
min = chmin(((s[n] - s[i]) - s[i]).abs, min)
end
puts minキーポイント
先に累積和を計算しておく。
累積和の基本についての解説はこちら
思考プロセス
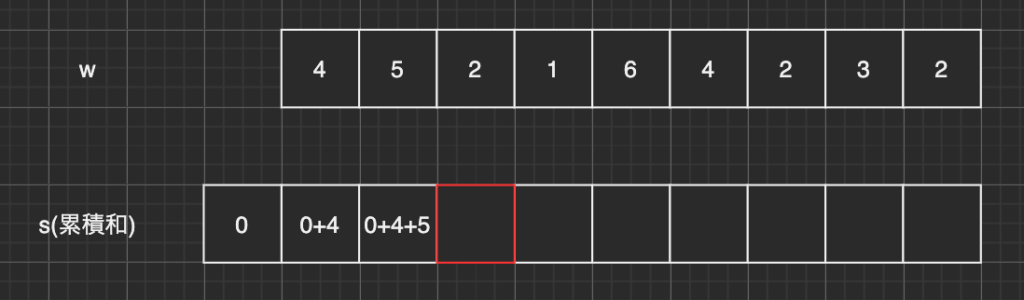
まずは、累積和を保存しておく、配列sを作りました。
大きさは元の大きさ+1が良さそうです。
s[i+1]にはs[i]とw[i]を足した結果を入れていきます。
例えば、赤枠のs[3]を求めるのであれば、s[3] = s[2] + w[2] = 0+4+5+2
今回は赤線の右と左の差が一番小さいの計算していくので、左側は、s[i]、右側はs[n] - s[i]となります。
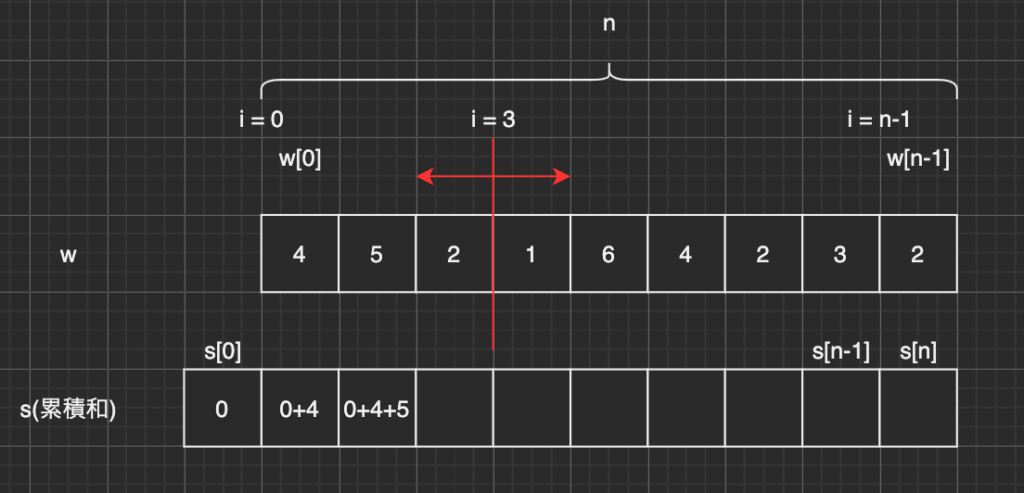
最後に1からn回ループして、赤線を右にずらして行って、最小の差を求めました。
もしかしたら1からn-1回まででよかったかもしれません。値が一個しかない場合を懸念して、nは残しておきました。
(0は左がなくなるので、差の値が大きいに決まっている。nは右がなくなるので、差の値が大きいに決まっている。)